What Is Radioactive Decay Apex
24.iii: Nuclear Reactions
- Page ID
- 6493
- To know the unlike kinds of radioactive decay.
- To remainder a nuclear reaction.
The 2 general kinds of nuclear reactions are nuclear decay reactions and nuclear transmutation reactions. In a nuclear decay reaction, likewise called radioactive decay, an unstable nucleus emits radiations and is transformed into the nucleus of one or more other elements. The resulting daughter nuclei accept a lower mass and are lower in energy (more stable) than the parent nucleus that rust-covered. In contrast, in a nuclear transmutation reaction, a nucleus reacts with a subatomic particle or another nucleus to form a product nucleus that is more massive than the starting material. As we shall see, nuclear decay reactions occur spontaneously nether all weather condition, but nuclear transmutation reactions occur just under very special conditions, such every bit the collision of a axle of highly energetic particles with a target nucleus or in the interior of stars. Nosotros brainstorm this section by considering the dissimilar classes of radioactive nuclei, along with their characteristic nuclear decay reactions and the radiation they emit.
Nuclear decay reactions occur spontaneously under all conditions, whereas nuclear transmutation reactions are induced.
Classes of Radioactive Nuclei
The three full general classes of radioactive nuclei are characterized by a unlike disuse process or set of processes:
- Neutron-rich nuclei. The nuclei on the upper left side of the band of stable nuclei have a neutron-to-proton ratio that is likewise high to requite a stable nucleus. These nuclei decay by a procedure that converts a neutron to a proton, thereby decreasing the neutron-to-proton ratio.
- Neutron-poor nuclei. Nuclei on the lower right side of the band of stable nuclei take a neutron-to-proton ratio that is too low to give a stable nucleus. These nuclei decay past processes that accept the net consequence of converting a proton to a neutron, thereby increasing the neutron-to-proton ratio.
- Heavy nuclei. With very few exceptions, heavy nuclei (those with A ≥ 200) are intrinsically unstable regardless of the neutron-to-proton ratio, and all nuclei with Z > 83 are unstable. This is presumably due to the cumulative effects of electrostatic repulsions between the large number of positively charged protons, which cannot be totally overcome by the strong nuclear strength, regardless of the number of neutrons nowadays. Such nuclei tend to decay by emitting an α particle (a helium nucleus, \(^4 _2 \textrm{He}\), which decreases the number of protons and neutrons in the original nucleus by 2. Because the neutron-to-proton ratio in an α particle is ane, the net effect of blastoff emission is an increment in the neutron-to-proton ratio.
Nuclear decay reactions e'er produce daughter nuclei that take a more than favorable neutron-to- proton ratio and hence are more stable than the parent nucleus.
Nuclear Decay Reactions
But equally we use the number and type of atoms nowadays to rest a chemical equation, we tin can use the number and type of nucleons present to write a balanced nuclear equation for a nuclear decay reaction. This procedure too allows united states of america to predict the identity of either the parent or the daughter nucleus if the identity of only one is known. Regardless of the mode of decay, the total number of nucleons is conserved in all nuclear reactions.
To describe nuclear decay reactions, chemists have extended the \(^A _Z \textrm{X}\) notation for nuclides to include radioactive emissions. Table \(\PageIndex{1}\) lists the name and symbol for each blazon of emitted radiation. The most notable add-on is the positron, a particle that has the aforementioned mass every bit an electron just a positive charge rather than a negative charge.
| Identity | Symbol | Charge | Mass (amu) |
|---|---|---|---|
| helium nucleus | \(^4_2\blastoff\) | +2 | iv.001506 |
| electron | \(^0_{-one}\beta\) or \(\beta ^-\) | −1 | 0.000549 |
| photon | \(_0^0\gamma\) | — | — |
| neutron | \(^1_0\textrm n\) | 0 | one.008665 |
| proton | \(^1_1\textrm p \) | +1 | 1.007276 |
| positron | \(^0_{+1}\beta\) or \(\beta ^+\) | +1 | 0.000549 |
Similar the notation used to signal isotopes, the upper left superscript in the symbol for a particle gives the mass number, which is the total number of protons and neutrons. For a proton or a neutron, A = one. Because neither an electron nor a positron contains protons or neutrons, its mass number is 0. The numbers should not be taken literally, however, as meaning that these particles have zero mass; ejection of a beta particle (an electron) only has a negligible result on the mass of a nucleus.
Similarly, the lower left subscript gives the charge of the particle. Because protons behave a positive accuse, Z = +1 for a proton. In contrast, a neutron contains no protons and is electrically neutral, so Z = 0. In the case of an electron, Z = −1, and for a positron, Z = +1. Because γ rays are high-energy photons, both A and Z are 0. In some cases, 2 unlike symbols are used for particles that are identical just produced in unlike means. For example, the symbol \(^0_{-1}\textrm e\), which is usually simplified to e−, represents a free electron or an electron associated with an cantlet, whereas the symbol \(^0_{-1}\beta\), which is often simplified to β−, denotes an electron that originates from within the nucleus, which is a β particle. Similarly, \(^4_{2}\textrm{He}^{2+}\) refers to the nucleus of a helium atom, and \(^4_{2}\alpha\) denotes an identical particle that has been ejected from a heavier nucleus.
In that location are six fundamentally different kinds of nuclear decay reactions, and each releases a unlike kind of particle or energy. The essential features of each reaction are shown in Figure \(\PageIndex{ane}\). The most mutual are alpha and beta decay and gamma emission, but the others are essential to an agreement of nuclear decay reactions.
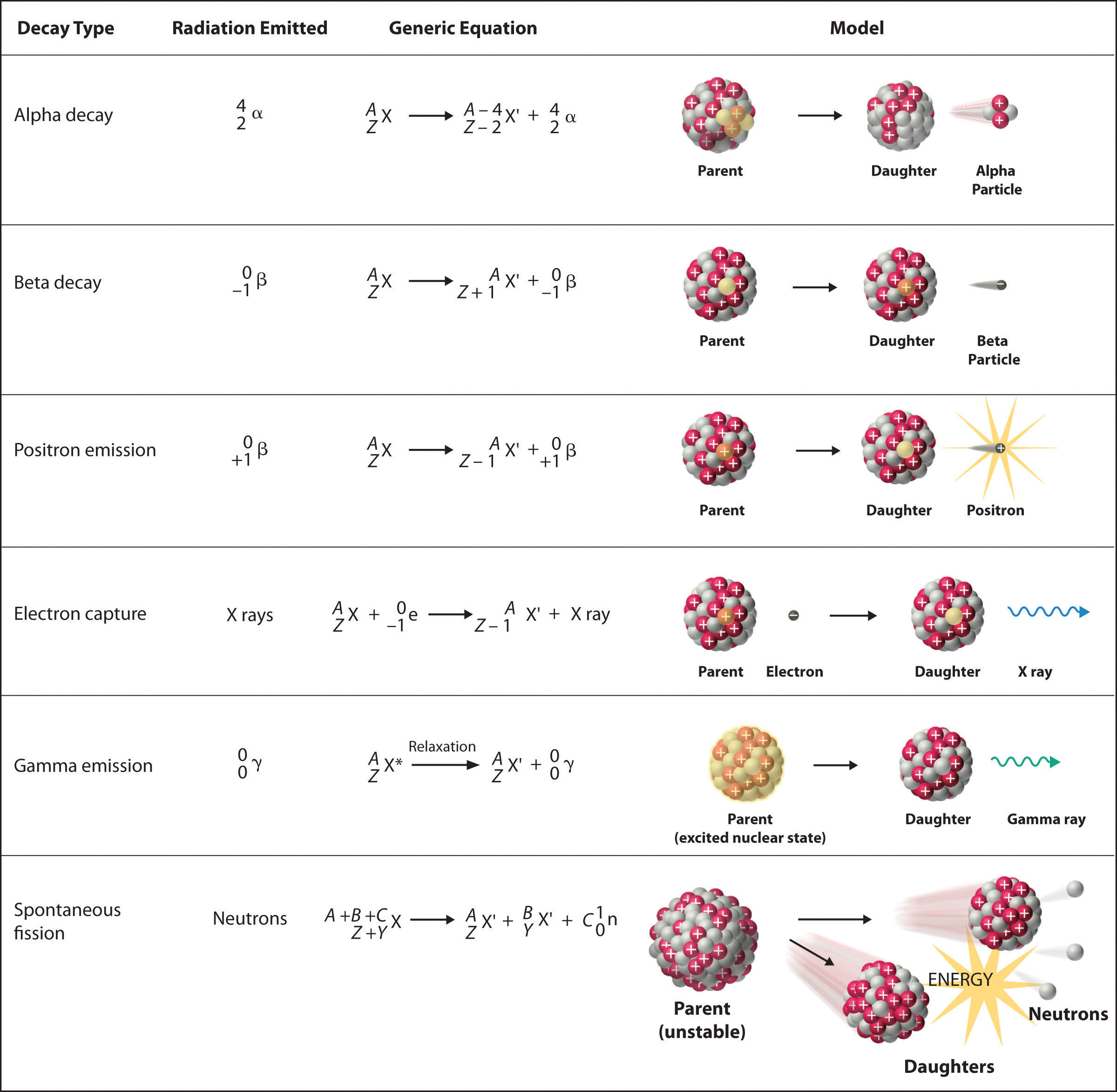
Alpha Decay
Many nuclei with mass numbers greater than 200 undergo alpha (α) decay, which results in the emission of a helium-4 nucleus equally an alpha (α) particle, \(^4_{two}\alpha\). The general reaction is as follows:
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A-four}_{Z-two} \textrm X'}+\underset{\textrm{alpha}\\ \textrm{particle}}{^4_2 \blastoff}\label{5.two.1}\]
The daughter nuclide contains ii fewer protons and ii fewer neutrons than the parent. Thus α-particle emission produces a daughter nucleus with a mass number A − iv and a nuclear accuse Z − 2 compared to the parent nucleus. Radium-226, for case, undergoes blastoff decay to form radon-222:
\[^{226}_{88}\textrm{Ra}\rightarrow ^{222}_{86}\textrm{Rn}+^{4}_{2}\blastoff\label{five.2.two}\]
Because nucleons are conserved in this and all other nuclear reactions, the sum of the mass numbers of the products, 222 + 4 = 226, equals the mass number of the parent. Similarly, the sum of the diminutive numbers of the products, 86 + 2 = 88, equals the atomic number of the parent. Thus the nuclear equation is counterbalanced.
Just as the total number of atoms is conserved in a chemical reaction, the total number of nucleons is conserved in a nuclear reaction.
Beta Decay
Nuclei that incorporate likewise many neutrons oft undergo beta (β) decay, in which a neutron is converted to a proton and a high-free energy electron that is ejected from the nucleus every bit a β particle:
\[\underset{\textrm{unstable} \\ \textrm{neutron in} \\ \textrm{nucleus}}{^1_0 \textrm north}\rightarrow \underset{\textrm{proton} \\ \textrm{retained} \\ \textrm{by nucleus}}{^{1}_{1} \textrm p}+\underset{\textrm{beta particle} \\ \textrm{emitted by} \\ \textrm{nucleus}}{^0_{-1} \beta}\label{5.2.3}\]
The full general reaction for beta decay is therefore
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z+one} \textrm X'}+\underset{\textrm{beta particle}}{^0_{-one} \beta}\label{5.ii.4}\]
Although beta decay does not change the mass number of the nucleus, it does effect in an increment of +1 in the atomic number because of the addition of a proton in the daughter nucleus. Thus beta decay decreases the neutron-to-proton ratio, moving the nucleus toward the band of stable nuclei. For example, carbon-xiv undergoes beta decay to class nitrogen-xiv:
\[^{14}_{6}\textrm{C}\rightarrow ^{14}_{7}\textrm{Northward}+\,^{0}_{-1}\beta\label{5.2.5}\]
Once once more, the number of nucleons is conserved, and the charges are balanced. The parent and the girl nuclei accept the same mass number, xiv, and the sum of the atomic numbers of the products is 6, which is the same as the atomic number of the carbon-14 parent.
Positron Emission
Because a positron has the same mass as an electron but opposite charge, positron emission is the contrary of beta decay. Thus positron emission is characteristic of neutron-poor nuclei, which disuse by transforming a proton to a neutron and emitting a high-energy positron:
\[^{1}_{1}\textrm{p}^+\rightarrow ^{i}_{0}\textrm{north}+\,^{0}_{+1}\beta^+\label{5.ii.6}\]
The general reaction for positron emission is therefore
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{girl}}{^{A}_{Z-1} \textrm Ten'}+\underset{\textrm{positron}}{^0_{+one} \beta^+}\label{5.2.7}\]
Like beta disuse, positron emission does not modify the mass number of the nucleus. In this instance, however, the atomic number of the daughter nucleus is lower by 1 than that of the parent. Thus the neutron-to-proton ratio has increased, again moving the nucleus closer to the band of stable nuclei. For instance, carbon-11 undergoes positron emission to class boron-11:
\[^{xi}_{6}\textrm{C}\rightarrow ^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta^+ \label{5.2.8}\]
Nucleons are conserved, and the charges balance. The mass number, 11, does not change, and the sum of the atomic numbers of the products is half dozen, the same every bit the diminutive number of the parent carbon-11 nuclide.
Electron Capture
A neutron-poor nucleus can disuse by either positron emission or electron capture (EC), in which an electron in an inner shell reacts with a proton to produce a neutron:
\[^{ane}_{1}\textrm{p} +\; ^{0}_{-1}\textrm{eastward}\rightarrow \, ^{1}_{0}\textrm due north\characterization{five.2.nine}\]
When a second electron moves from an outer vanquish to take the place of the lower-free energy electron that was absorbed by the nucleus, an ten-ray is emitted. The overall reaction for electron capture is thus
\[\underset{\textrm{parent}}{^A_Z \textrm 10}+\underset{\textrm{electron}}{^0_{-ane} \textrm e}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\textrm{x-ray}\characterization{5.two.10}\]
Electron capture does non change the mass number of the nucleus considering both the proton that is lost and the neutron that is formed have a mass number of 1. As with positron emission, however, the atomic number of the daughter nucleus is lower past 1 than that of the parent. Once once more, the neutron-to-proton ratio has increased, moving the nucleus toward the band of stable nuclei. For case, iron-55 decays by electron capture to form manganese-55, which is frequently written equally follows:
\[^{55}_{26}\textrm{Fe}\overset{\textrm{EC}}{\rightarrow}\, ^{55}_{25}\textrm{Mn}+\textrm{x-ray}\characterization{5.two.xi}\]
The diminutive numbers of the parent and daughter nuclides differ in Equation 20.2.11, although the mass numbers are the same. To write a balanced nuclear equation for this reaction, we must explicitly include the captured electron in the equation:
\[^{55}_{26}\textrm{Iron}+\,^{0}_{-1}\textrm{e}\rightarrow \, ^{55}_{25}\textrm{Mn}+\textrm{x-ray}\label{5.two.12}\]
Both positron emission and electron capture are usually observed for nuclides with low neutron-to-proton ratios, but the decay rates for the two processes tin can be very different.
Gamma Emission
Many nuclear disuse reactions produce daughter nuclei that are in a nuclear excited state, which is similar to an atom in which an electron has been excited to a higher-energy orbital to give an electronic excited state. Just as an electron in an electronic excited state emits energy in the form of a photon when information technology returns to the basis state, a nucleus in an excited country releases energy in the form of a photon when it returns to the footing country. These high-energy photons are γ rays. Gamma (\(\gamma\)) emission tin occur virtually instantaneously, as it does in the alpha decay of uranium-238 to thorium-234, where the asterisk denotes an excited state:
\[^{238}_{92}\textrm{U}\rightarrow \, \underset{\textrm{excited} \\ \textrm{nuclear} \\ \textrm{country}}{^{234}_{90}\textrm{Thursday*}} + ^{4}_{2}\blastoff\xrightarrow {\textrm{relaxation}\,}\,^{234}_{ninety}\textrm{Th}+^{0}_{0}\gamma\label{5.two.13}\]
If we disregard the decay issue that created the excited nucleus, and then
\[^{234}_{88}\textrm{Thursday*} \rightarrow\, ^{234}_{88}\textrm{Th}+^{0}_{0}\gamma\label{5.2.xiv}\]
or more than by and large,
\[^{A}_{Z}\textrm{Ten*} \rightarrow\, ^{A}_{Z}\textrm{X}+^{0}_{0}\gamma\characterization{five.2.15}\]
Gamma emission can also occur after a meaning filibuster. For example, technetium-99m has a one-half-life of about half dozen hours before emitting a γ ray to class technetium-99 (the m is for metastable). Because γ rays are energy, their emission does not affect either the mass number or the atomic number of the daughter nuclide. Gamma-ray emission is therefore the just kind of radiation that does not necessarily involve the conversion of one element to some other, although it is well-nigh e'er observed in conjunction with some other nuclear decay reaction.
Spontaneous Fission
Merely very massive nuclei with high neutron-to-proton ratios can undergo spontaneous fission, in which the nucleus breaks into two pieces that take different atomic numbers and atomic masses. This process is most important for the transactinide elements, with Z ≥ 104. Spontaneous fission is invariably accompanied past the release of large amounts of free energy, and information technology is unremarkably accompanied past the emission of several neutrons as well. An instance is the spontaneous fission of \(^{254}_{98}\textrm{Cf}\), which gives a distribution of fission products; 1 possible ready of products is shown in the following equation:
\[^{254}_{98}\textrm{Cf}\rightarrow \,^{118}_{46}\textrm{Pd}+\,^{132}_{52}\textrm{Te}+4^{1}_{0}\textrm{n}\label{five.2.xvi}\]
Once again, the number of nucleons is conserved. Thus the sum of the mass numbers of the products (118 + 132 + iv = 254) equals the mass number of the reactant. Similarly, the sum of the atomic numbers of the products [46 + 52 + (iv × 0) = 98] is the aforementioned as the atomic number of the parent nuclide.
Write a counterbalanced nuclear equation to describe each reaction.
- the beta decay of \(^{35}_{16}\textrm{South}\)
- the decay of \(^{201}_{80}\textrm{Hg}\) by electron capture
- the decay of \(^{xxx}_{15}\textrm{P}\) by positron emission
Given: radioactive nuclide and fashion of disuse
Asked for: balanced nuclear equation
Strategy:
A Identify the reactants and the products from the information given.
B Use the values of A and Z to identify any missing components needed to residue the equation.
Solution
a.
A Nosotros know the identities of the reactant and one of the products (a β particle). We can therefore begin by writing an equation that shows the reactant and i of the products and indicates the unknown product as \(^{A}_{Z}\textrm{Ten}\):
\[^{35}_{sixteen}\textrm{S}\rightarrow\,^{A}_{Z}\textrm{Ten}+\,^{0}_{-i}\beta\]
B Because both protons and neutrons must be conserved in a nuclear reaction, the unknown product must have a mass number of A = 35 − 0 = 35 and an atomic number of Z = xvi − (−1) = 17. The element with Z = 17 is chlorine, so the balanced nuclear equation is as follows:
\[^{35}_{sixteen}\textrm{Southward}\rightarrow\,^{35}_{17}\textrm{Cl}+\,^{0}_{-1}\beta\]
b.
A We know the identities of both reactants: \(^{201}_{80}\textrm{Hg}\) and an inner electron, \(^{0}_{-1}\textrm{e}\). The reaction is as follows:
\(^{201}_{80}\textrm{Hg}+\,^{0}_{-ane}\textrm due east\rightarrow\,^{A}_{Z}\textrm{X}\)
B Both protons and neutrons are conserved, then the mass number of the product must be A = 201 + 0 = 201, and the atomic number of the product must be Z = lxxx + (−i) = 79, which corresponds to the chemical element gold. The balanced nuclear equation is thus
\(^{201}_{lxxx}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{201}_{79}\textrm{Au}\)
c.
A As in role (a), we are given the identities of the reactant and one of the products—in this case, a positron. The unbalanced nuclear equation is therefore
\(^{thirty}_{fifteen}\textrm{P}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{+1}\beta\)
B The mass number of the 2d product is A = thirty − 0 = thirty, and its atomic number is Z = fifteen − 1 = fourteen, which corresponds to silicon. The balanced nuclear equation for the reaction is as follows:
\(^{30}_{15}\textrm{P}\rightarrow\,^{xxx}_{14}\textrm{Si}+\,^{0}_{+1}\beta\)
Write a counterbalanced nuclear equation to describe each reaction.
- \(^{eleven}_{vi}\textrm{C}\) by positron emission
- the beta decay of molybdenum-99
- the emission of an α particle followed past gamma emission from \(^{185}_{74}\textrm{W}\)
Answer
- \(^{xi}_{6}\textrm{C}\rightarrow\,^{11}_{five}\textrm{B}+\,^{0}_{+i}\beta\)
- \(^{99}_{42}\textrm{Mo}\rightarrow\,^{99m}_{43}\textrm{Tc}+\,^{0}_{-1}\beta\)
- \(^{185}_{74}\textrm{W}\rightarrow\,^{181}_{72}\textrm{Hf}+\,^{4}_{ii}\alpha +\,^{0}_{0}\gamma\)
Predict the kind of nuclear change each unstable nuclide undergoes when information technology decays.
- \(^{45}_{22}\textrm{Ti}\)
- \(^{242}_{94}\textrm{Pu}\)
- \(^{12}_{5}\textrm{B}\)
- \(^{256}_{100}\textrm{Fm}\)
Given: nuclide
Asked for: type of nuclear disuse
Strategy:
Based on the neutron-to-proton ratio and the value of Z, predict the type of nuclear decay reaction that volition produce a more stable nuclide.
Solution
- This nuclide has a neutron-to-proton ratio of but ane.05, which is much less than the requirement for stability for an chemical element with an atomic number in this range. Nuclei that have low neutron-to-proton ratios disuse by converting a proton to a neutron. The two possibilities are positron emission, which converts a proton to a neutron and a positron, and electron capture, which converts a proton and a core electron to a neutron. In this case, both are observed, with positron emission occurring about 86% of the fourth dimension and electron capture nigh 14% of the time.
- Nuclei with Z > 83 are likewise heavy to be stable and usually undergo alpha decay, which decreases both the mass number and the atomic number. Thus \(^{242}_{94}\textrm{Pu}\) is expected to decay by alpha emission.
- This nuclide has a neutron-to-proton ratio of one.4, which is very high for a light element. Nuclei with high neutron-to-proton ratios decay by converting a neutron to a proton and an electron. The electron is emitted every bit a β particle, and the proton remains in the nucleus, causing an increment in the atomic number with no change in the mass number. We therefore predict that \(^{12}_{five}\textrm{B}\) will undergo beta decay.
- This is a massive nuclide, with an atomic number of 100 and a mass number much greater than 200. Nuclides with A ≥ 200 tend to decay by alpha emission, and fifty-fifty heavier nuclei tend to undergo spontaneous fission. Nosotros therefore predict that \(^{256}_{100}\textrm{Fm}\) volition decay by either or both of these two processes. In fact, it decays by both spontaneous fission and blastoff emission, in a 97:iii ratio.
Predict the kind of nuclear alter each unstable nuclide undergoes when it decays.
- \(^{32}_{14}\textrm{Si}\)
- \(^{43}_{21}\textrm{Sc}\)
- \(^{231}_{91}\textrm{Pa}\)
Answer
- beta decay
- positron emission or electron capture
- alpha decay
Radioactivity Series
The nuclei of all elements with atomic numbers greater than 83 are unstable. Thus all isotopes of all elements beyond bismuth in the periodic table are radioactive. Considering alpha decay decreases Z by but 2, and positron emission or electron capture decreases Z by only i, information technology is incommunicable for whatever nuclide with Z > 85 to decay to a stable daughter nuclide in a unmarried step, except via nuclear fission. Consequently, radioactive isotopes with Z > 85 usually decay to a daughter nucleus that is radiaoctive, which in turn decays to a second radioactive daughter nucleus, and then forth, until a stable nucleus finally results. This series of sequential alpha- and beta-disuse reactions is called a radioactivity series. The most common is the uranium-238 decay series, which produces lead-206 in a series of fourteen sequential alpha- and beta-decay reactions (Effigy \(\PageIndex{two}\)). Although a radioactive decay serial can exist written for almost any isotope with Z > 85, only two others occur naturally: the decay of uranium-235 to lead-207 (in 11 steps) and thorium-232 to lead-208 (in 10 steps). A 4th series, the disuse of neptunium-237 to bismuth-209 in 11 steps, is known to accept occurred on the primitive Globe. With a half-life of "only" two.14 million years, all the neptunium-237 present when Globe was formed rust-covered long agone, and today all the neptunium on Globe is synthetic.
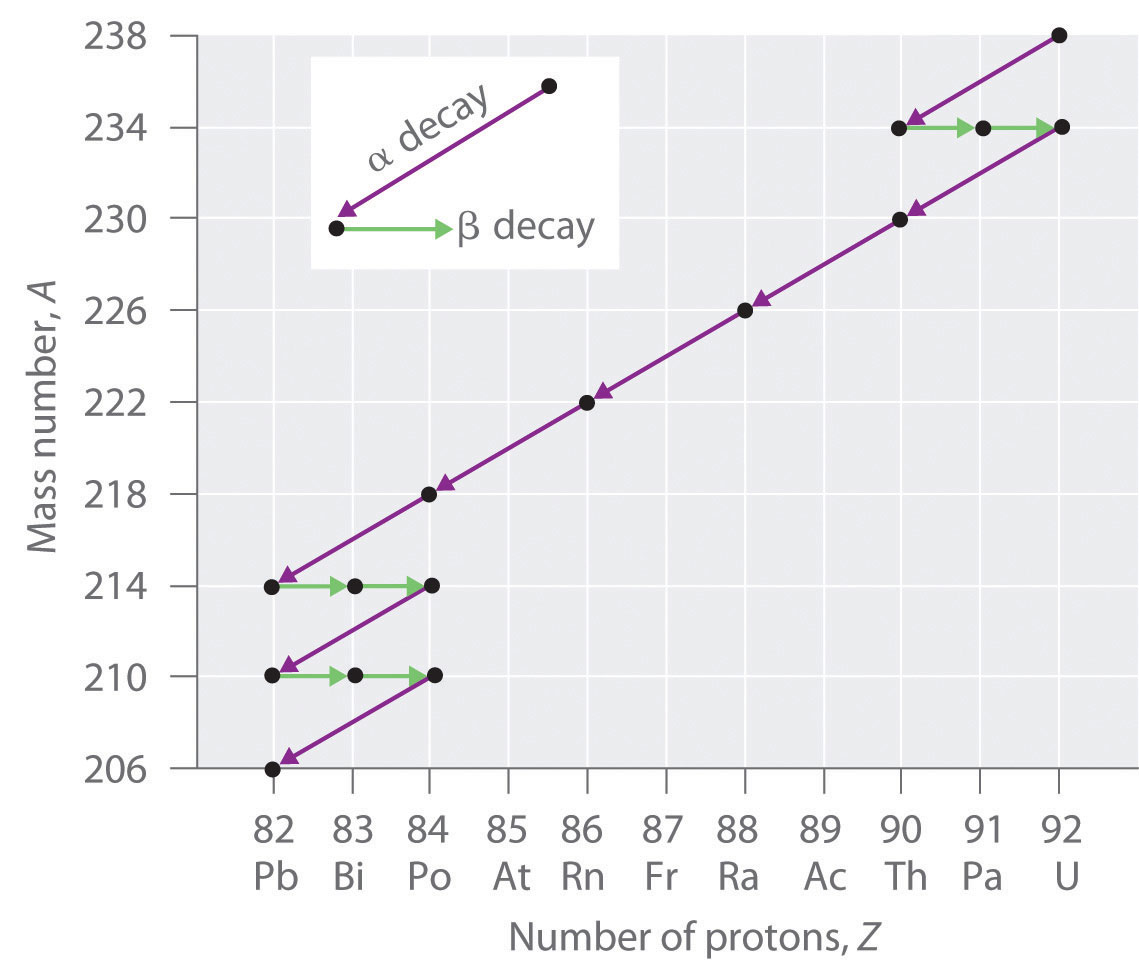
Due to these radioactive decay series, small amounts of very unstable isotopes are found in ores that contain uranium or thorium. These rare, unstable isotopes should have decayed long ago to stable nuclei with a lower atomic number, and they would no longer exist found on Earth. Considering they are generated continuously by the decay of uranium or thorium, however, their amounts have reached a steady land, in which their rate of germination is equal to their rate of disuse. In some cases, the abundance of the daughter isotopes tin can exist used to date a material or place its origin.
Induced Nuclear Reactions
The discovery of radioactive decay in the late 19th century showed that some nuclei spontaneously transform into nuclei with a different number of protons, thereby producing a unlike element. When scientists realized that these naturally occurring radioactive isotopes rust-covered by emitting subatomic particles, they realized that—in principle—it should be possible to carry out the reverse reaction, converting a stable nucleus to another more massive nucleus by bombarding information technology with subatomic particles in a nuclear transmutation reaction.
The first successful nuclear transmutation reaction was carried out in 1919 by Ernest Rutherford, who showed that α particles emitted by radium could react with nitrogen nuclei to course oxygen nuclei. As shown in the following equation, a proton is emitted in the process:
\[^{4}_{2}\blastoff + \, ^{14}_{7}\textrm{N} \rightarrow \,^{17}_{eight}\textrm{O}+\,^{1}_{one}\textrm{p}\label{5.2.17}\]
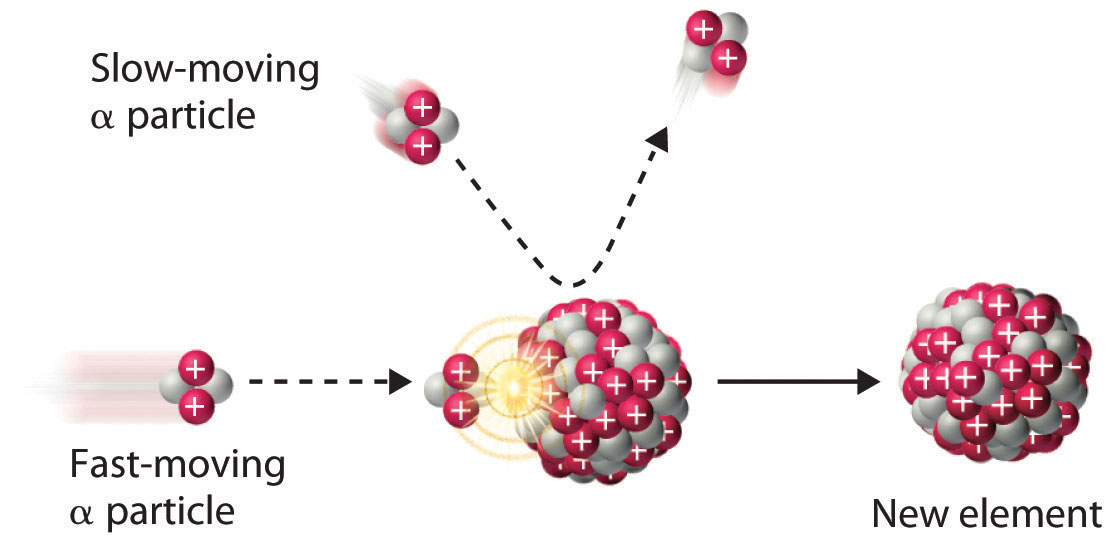
Rutherford'south nuclear transmutation experiments led to the discovery of the neutron. He plant that bombarding the nucleus of a light target chemical element with an α particle usually converted the target nucleus to a production that had an diminutive number higher by one and a mass number higher past iii than the target nucleus. Such behavior is consistent with the emission of a proton after reaction with the α particle. Very light targets such every bit Li, Exist, and B reacted differently, however, emitting a new kind of highly penetrating radiation rather than a proton. Because neither a magnetic field nor an electrical field could deflect these loftier-energy particles, Rutherford ended that they were electrically neutral. Other observations suggested that the mass of the neutral particle was similar to the mass of the proton. In 1932, James Chadwick (Nobel Prize in Physics, 1935), who was a student of Rutherford's at the time, named these neutral particles neutrons and proposed that they were fundamental building blocks of the atom. The reaction that Chadwick initially used to explain the production of neutrons was as follows:
\[^{iv}_{2}\alpha + \, ^{9}_{4}\textrm{Be} \rightarrow \,^{12}_{half dozen}\textrm{C}+\,^{1}_{0}\textrm{northward}\label{v.ii.18}\]
Because α particles and atomic nuclei are both positively charged, electrostatic forces cause them to repel each other. Just α particles with very high kinetic energy can overcome this repulsion and collide with a nucleus (Effigy \(\PageIndex{3}\)). Neutrons have no electric charge, nonetheless, so they are not repelled by the nucleus. Hence battery with neutrons is a much easier style to gear up new isotopes of the lighter elements. In fact, carbon-fourteen is formed naturally in the atmosphere by bombarding nitrogen-14 with neutrons generated by cosmic rays:
\[^{ane}_{0}\textrm{n} + \, ^{fourteen}_{7}\textrm{N} \rightarrow \,^{14}_{6}\textrm{C}+\,^{1}_{one}\textrm{p}\label{5.ii.19}\]
In 1933, Frédéric Joliot and Iréne Joliot-Curie (daughter of Marie and Pierre Curie) prepared the offset artificial radioactive isotope by bombarding aluminum-27 with α particles. For each 27Al that reacted, i neutron was released. Identify the product nuclide and write a balanced nuclear equation for this transmutation reaction.
Given: reactants in a nuclear transmutation reaction
Asked for: product nuclide and counterbalanced nuclear equation
Strategy:
A Based on the reactants and one production, identify the other production of the reaction. Apply conservation of mass and charge to make up one's mind the values of Z and A of the product nuclide and thus its identity.
B Write the balanced nuclear equation for the reaction.
Solution
A Bombarding an element with α particles normally produces an element with an atomic number that is ii greater than the diminutive number of the target nucleus. Thus we expect that aluminum (Z = 13) volition be converted to phosphorus (Z = 15). With 1 neutron released, conservation of mass requires that the mass number of the other product exist 3 greater than the mass number of the target. In this instance, the mass number of the target is 27, then the mass number of the product will be 30. The second product is therefore phosphorus-thirty, \(^{30}_{fifteen}\textrm{P}\).
B The balanced nuclear equation for the reaction is as follows:
\[^{27}_{13}\textrm{Al} + \, ^{4}_{2}\alpha \rightarrow \,^{30}_{fifteen}\textrm{P}+\,^{1}_{0}\textrm{due north}\]
Because all isotopes of technetium are radioactive and have curt half-lives, it does not exist in nature. Technetium can, yet, exist prepared by nuclear transmutation reactions. For case, bombarding a molybdenum-96 target with deuterium nuclei \((^{two}_{1}\textrm{H})\) produces technetium-97. Identify the other product of the reaction and write a balanced nuclear equation for this transmutation reaction.
Answer
neutron, \(^{1}_{0}\textrm{n}\); \(^{96}_{42}\textrm{Mo} + \, ^{2}_{1}\textrm{H} \rightarrow \,^{97}_{43}\textrm{Tc}+\,^{1}_{0}\textrm{n}\)
We noted before in this section that very heavy nuclides, corresponding to Z ≥ 104, tend to decay by spontaneous fission. Nuclides with slightly lower values of Z, such as the isotopes of uranium (Z = 92) and plutonium (Z = 94), do not undergo spontaneous fission at whatever significant rate. Some isotopes of these elements, all the same, such as \(^{235}_{92}\textrm{U}\) and \(^{239}_{94}\textrm{Pu}\) undergo induced nuclear fission when they are bombarded with relatively depression-free energy neutrons, every bit shown in the post-obit equation for uranium-235 and in Figure \(\PageIndex{3}\):
\[^{235}_{92}\textrm{U} + \, ^{i}_{0}\textrm{n} \rightarrow \,^{236}_{92}\textrm{U}\rightarrow \,^{141}_{56}\textrm{Ba}+\,^{92}_{36}\textrm{Kr}+iii^{1}_{0}\textrm{n}\label{5.2.20}\]
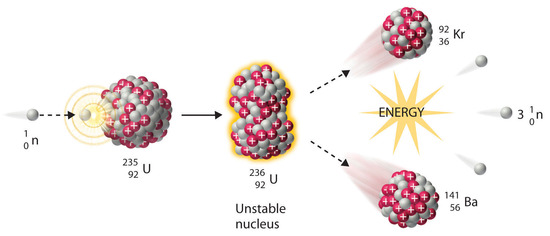
Whatever isotope that can undergo a nuclear fission reaction when bombarded with neutrons is called a fissile isotope.
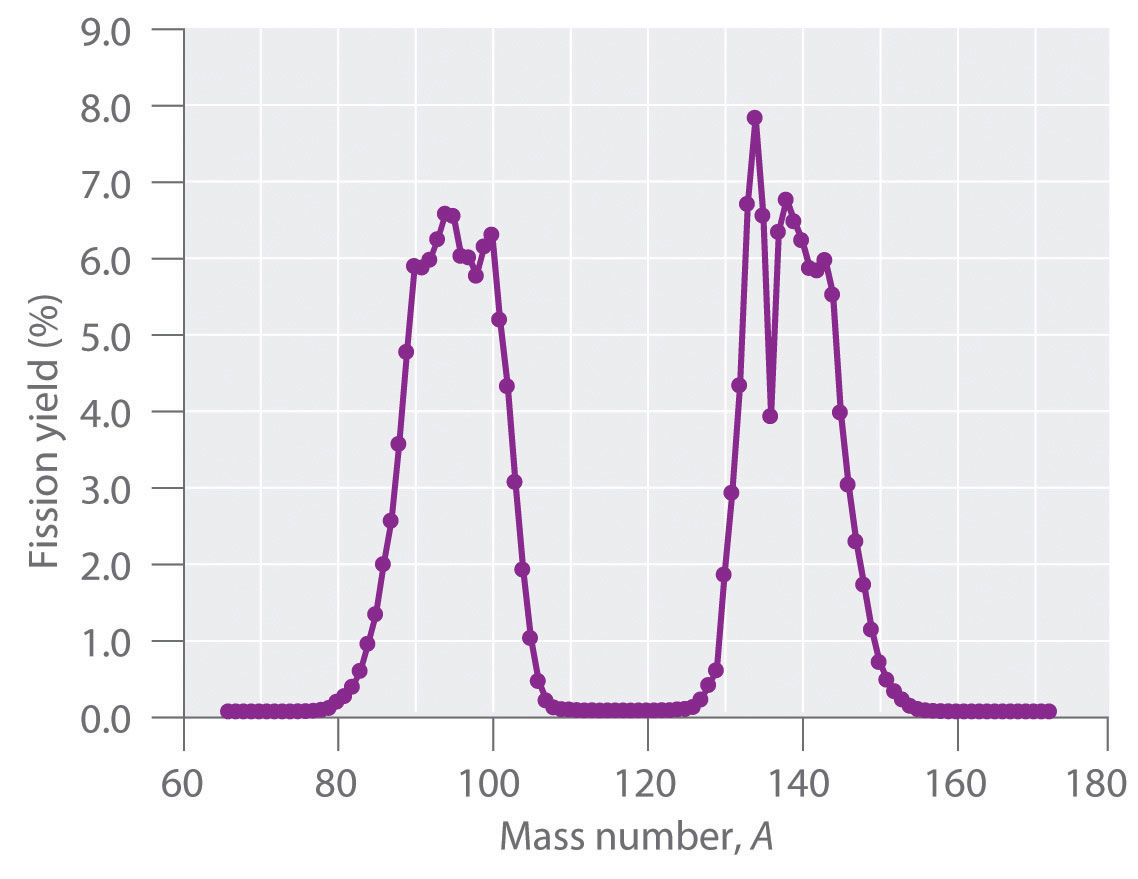
During nuclear fission, the nucleus usually divides asymmetrically rather than into 2 equal parts, as shown in Figure \(\PageIndex{four}\). Moreover, every fission effect of a given nuclide does not give the same products; more than than l different fission modes have been identified for uranium-235, for example. Consequently, nuclear fission of a fissile nuclide can never exist described by a unmarried equation. Instead, equally shown in Figure \(\PageIndex{5}\), a distribution of many pairs of fission products with different yields is obtained, just the mass ratio of each pair of fission products produced by a unmarried fission event is always roughly 3:2.
Synthesis of Transuranium Elements
Uranium (Z = 92) is the heaviest naturally occurring element. Consequently, all the elements with Z > 92, the transuranium elements, are artificial and have been prepared by bombarding suitable target nuclei with smaller particles. The first of the transuranium elements to be prepared was neptunium (Z = 93), which was synthesized in 1940 by bombarding a 238U target with neutrons. As shown in Equation 20.21, this reaction occurs in two steps. Initially, a neutron combines with a 238U nucleus to course 239U, which is unstable and undergoes beta decay to produce 239Np:
\(^{238}_{92}\textrm{U} + \, ^{ane}_{0}\textrm{n} \rightarrow \,^{239}_{92}\textrm{U}\rightarrow \,^{239}_{93}\textrm{Np}+\,^{0}_{-i}\beta\characterization{5.two.21}\)
Subsequent beta disuse of 239Np produces the 2d transuranium element, plutonium (Z = 94):
\(^{239}_{93}\textrm{Np} \rightarrow \,^{239}_{94}\textrm{Pu}+\,^{0}_{-1}\beta\label{v.2.22}\)
Bombarding the target with more massive nuclei creates elements that have atomic numbers significantly greater than that of the target nucleus (Table \(\PageIndex{2}\)). Such techniques take resulted in the creation of the superheavy elements 114 and 116, both of which lie in or well-nigh the "island of stability."
| \(^{239}_{94}\textrm{Pu}+\,^{iv}_{2}\alpha \rightarrow \,^{242}_{96}\textrm{Cm}+\,^{1}_{0}\textrm{north}\) |
| \(^{239}_{94}\textrm{Pu}+\,^{4}_{ii}\alpha \rightarrow \,^{241}_{95}\textrm{Am}+\,^{ane}_{ane}\textrm{p}+\,^{1}_{0}\textrm{n}\) |
| \(^{242}_{96}\textrm{Cm}+\,^{4}_{2}\alpha \rightarrow \,^{243}_{97}\textrm{Bk}+\,^{one}_{one}\textrm{p}+2^{i}_{0}\textrm{n}\) |
| \(^{253}_{99}\textrm{Es}+\,^{four}_{2}\alpha \rightarrow \,^{256}_{101}\textrm{Md}+\,^{1}_{0}\textrm{n}\) |
| \(^{238}_{92}\textrm{U}+\,^{12}_{half dozen}\textrm{C} \rightarrow \,^{246}_{98}\textrm{Cf}+4^{i}_{0}\textrm{northward}\) |
| \(^{252}_{98}\textrm{Cf}+\,^{10}_{5}\textrm{B} \rightarrow \,^{256}_{103}\textrm{Lr}+6^{1}_{0}\textrm{northward}\) |
A device chosen a particle accelerator is used to accelerate positively charged particles to the speeds needed to overcome the electrostatic repulsions between them and the target nuclei past using electrical and magnetic fields. Operationally, the simplest particle accelerator is the linear accelerator (Effigy \(\PageIndex{6}\)), in which a axle of particles is injected at one terminate of a long evacuated tube. Rapid alternation of the polarity of the electrodes along the tube causes the particles to exist alternately accelerated toward a region of opposite charge and repelled by a region with the same charge, resulting in a tremendous acceleration every bit the particle travels downwards the tube. A mod linear accelerator such as the Stanford Linear Accelerator (SLAC) at Stanford University is about two miles long.
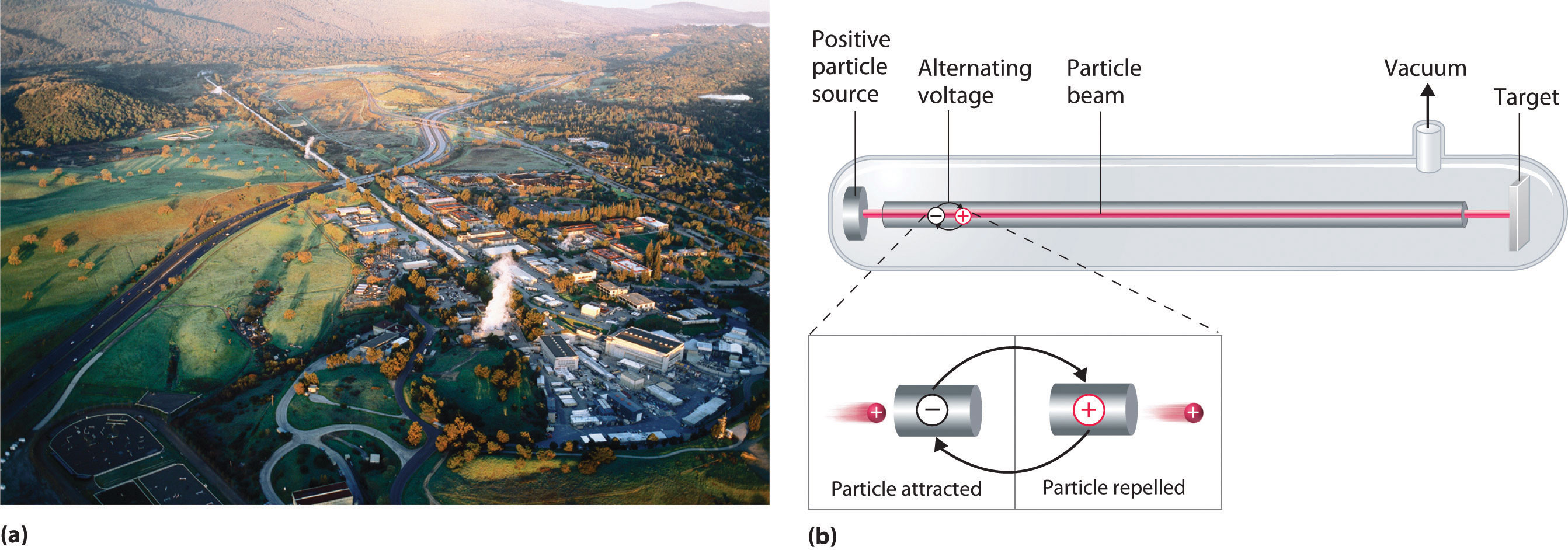
To achieve the aforementioned outcome in less space, a particle accelerator called a cyclotron forces the charged particles to travel in a round path rather than a linear one. The particles are injected into the center of a band and accelerated by rapidly alternating the polarity of 2 large D-shaped electrodes above and below the ring, which accelerates the particles outward along a spiral path toward the target.
The length of a linear accelerator and the size of the D-shaped electrodes in a cyclotron severely limit the kinetic free energy that particles can accomplish in these devices. These limitations tin be overcome by using a synchrotron, a hybrid of the two designs. A synchrotron contains an evacuated tube like to that of a linear accelerator, just the tube is circular and can be more than a mile in diameter. Charged particles are accelerated around the circumvolve past a series of magnets whose polarities chop-chop alternating.
Summary
In nuclear disuse reactions (or radioactive decay), the parent nucleus is converted to a more stable daughter nucleus. Nuclei with too many neutrons disuse past converting a neutron to a proton, whereas nuclei with likewise few neutrons decay by converting a proton to a neutron. Very heavy nuclei (with A ≥ 200 and Z > 83) are unstable and tend to decay by emitting an α particle. When an unstable nuclide undergoes radioactivity, the total number of nucleons is conserved, as is the total positive charge. 6 different kinds of nuclear decay reactions are known. Blastoff disuse results in the emission of an α particle, \(^4 _2 \alpha\), and produces a daughter nucleus with a mass number that is lower by 4 and an atomic number that is lower by 2 than the parent nucleus. Beta decay converts a neutron to a proton and emits a loftier-energy electron, producing a girl nucleus with the same mass number as the parent and an atomic number that is higher by i. Positron emission is the opposite of beta decay and converts a proton to a neutron plus a positron. Positron emission does not modify the mass number of the nucleus, but the atomic number of the daughter nucleus is lower by one than the parent. In electron capture (EC), an electron in an inner shell reacts with a proton to produce a neutron, with emission of an 10-ray. The mass number does not modify, but the atomic number of the daughter is lower by 1 than the parent. In gamma emission, a girl nucleus in a nuclear excited state undergoes a transition to a lower-free energy land past emitting a γ ray. Very heavy nuclei with high neutron-to-proton ratios tin can undergo spontaneous fission, in which the nucleus breaks into two pieces that can accept different atomic numbers and atomic masses with the release of neutrons. Many very heavy nuclei decay via a radioactivity series—a succession of some combination of alpha- and beta-decay reactions. In nuclear transmutation reactions, a target nucleus is bombarded with energetic subatomic particles to requite a product nucleus that is more massive than the original. All transuranium elements—elements with Z > 92—are artificial and must be prepared past nuclear transmutation reactions. These reactions are carried out in particle accelerators such as linear accelerators, cyclotrons, and synchrotrons.
Key Takeaway
Nuclear decay reactions occur spontaneously under all weather and produce more stable girl nuclei, whereas nuclear transmutation reactions are induced and grade a production nucleus that is more massive than the starting material.
Primal Equations
alpha disuse
Equation 20.1: \(^A_Z \textrm X\rightarrow \, ^{A-iv}_{Z-2} \textrm X'+\,^4_2 \alpha\)
beta disuse
Equation xx.4: \(^A_Z \textrm Ten\rightarrow \, ^{A}_{Z+one} \textrm Ten'+\,^0_{-i} \beta\)
positron emission
Equation 20.7: \(^A_Z \textrm X\rightarrow \, ^{A}_{Z-one} \textrm X'+\,^0_{+i} \beta\)
electron capture
Equation 20.10: \(^A_Z \textrm 10+\,^{0}_{-i} \textrm e\rightarrow \, ^{A}_{Z-1} \textrm 10'+\textrm{x-ray}\)
gamma emission
Equation 20.15: \(^A_Z \textrm{10*}\rightarrow \, ^{A}_{Z} \textrm X+\,^0_{0} \gamma\)
What Is Radioactive Decay Apex,
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Book:_General_Chemistry:_Principles_Patterns_and_Applications_%28Averill%29/24:_Nuclear_Chemistry/24.03:_Nuclear_Reactions
Posted by: gonzalezhounnenst.blogspot.com


0 Response to "What Is Radioactive Decay Apex"
Post a Comment